激活函数的作用
给神经元引入非线性因素,使得网络可以逼近任意的非线性函数,具有更强的泛化能力
不同的激活函数
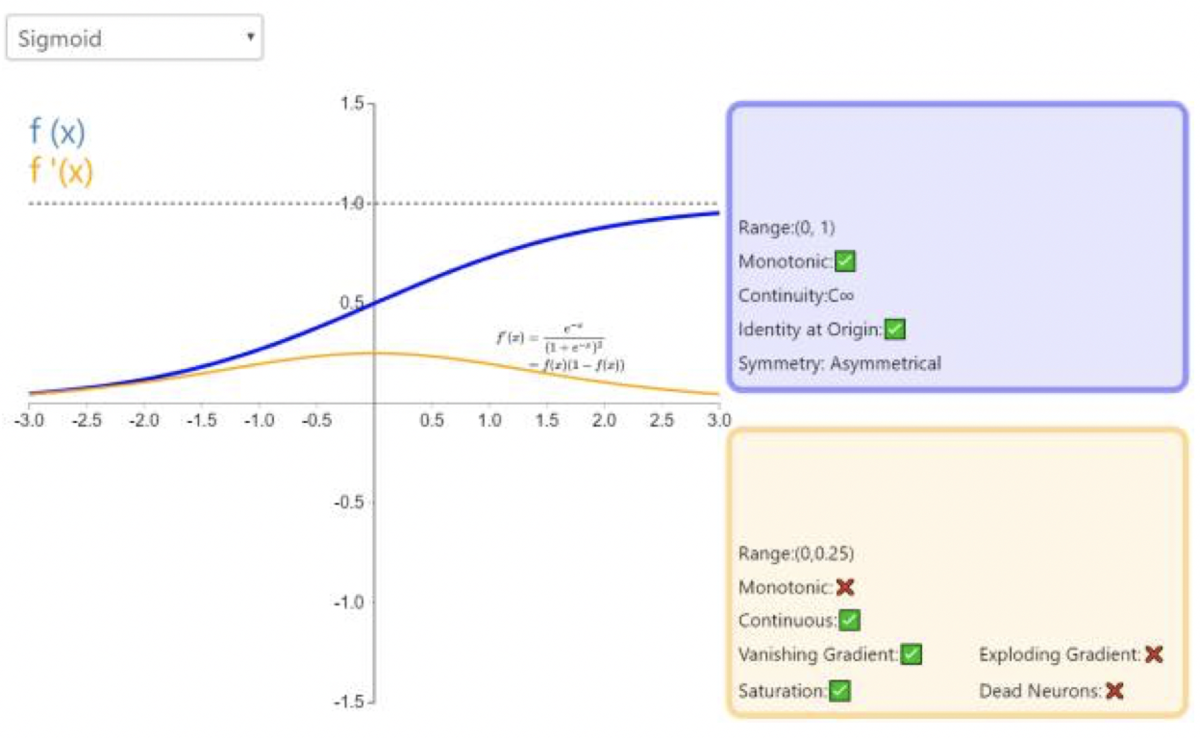
Sigmoid
S(x)=1+e−x1
函数图像:
![]()
缺点:
- 计算量大(指数运算)
- 反向传播时容易出现梯度消失问题(导数从0开始很快又趋近于0)
- 输出在0-1之间,训练缓慢
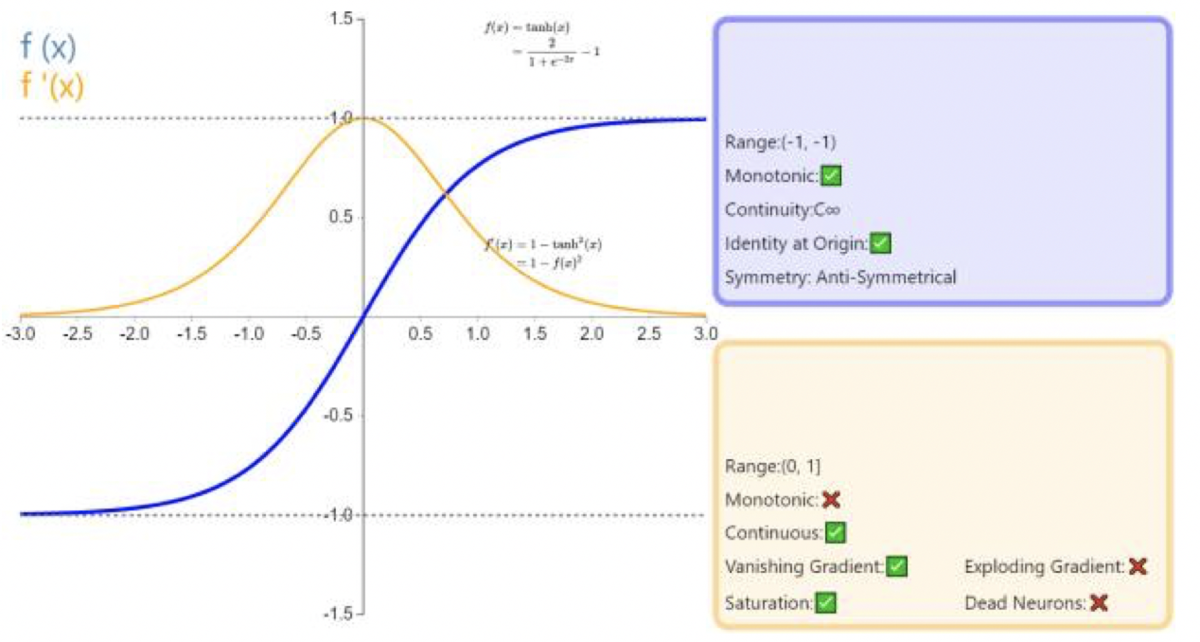
Tanh
f(z)=tanh(z)=ez+e−zez−e−z
tanh(z)=2sigmoid(2z)−1
函数图像:
![]()
优点:
缺点:
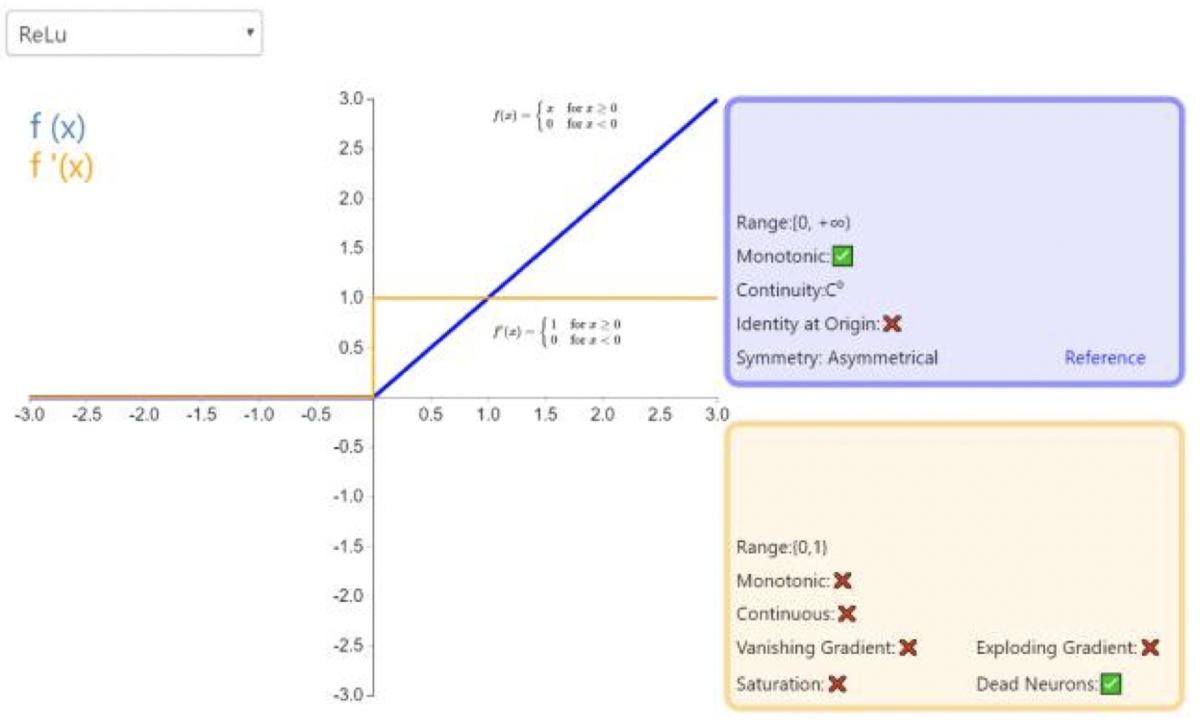
ReLU
f(x)={x0ifx≥0ifx<0
函数图像:
![]()
优点:
- 解决了部分梯度消失问题(输入为正时)
- 计算更快(函数简单)
- 收敛更快
缺点:
PReLU、Leaky ReLU、RRelu
PReLU: Parametric Rectified Linear Unit
RReLU: Randomized Leaky Rectified Linear Unit
f(xi)={xiaixiifxi≥0ifxi<0
![]()
优点:
三种ReLU的比较:
- 若ai=0,则PReLU退化为ReLU
- Leaky ReLU中的ai是一个很小的固定值
- PReLU中的ai是根据数据变化的
- RReLU中的ai在训练阶段是一个在给定范围内随机抽取的值,在测试阶段会固定下来
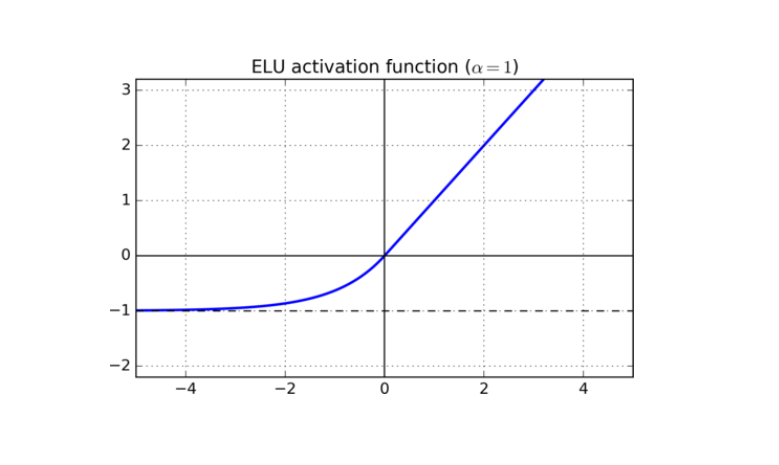
ELU
ELU: Exponential Linear Units
f(x)={xα(ex−1)ifx≥0ifx<0
函数图像:
![]()
优点:
- 包含ReLU的所有优点
- 神经元不会死亡
- 输出均值接近于0
缺点:
Maxout
f(x)=maxj∈[1,k]zij=max(w1Tx+b1,w2Tx+b2,...,wkTx+bk)
即对于某一层神经网络,将激活值最大的作为输出。
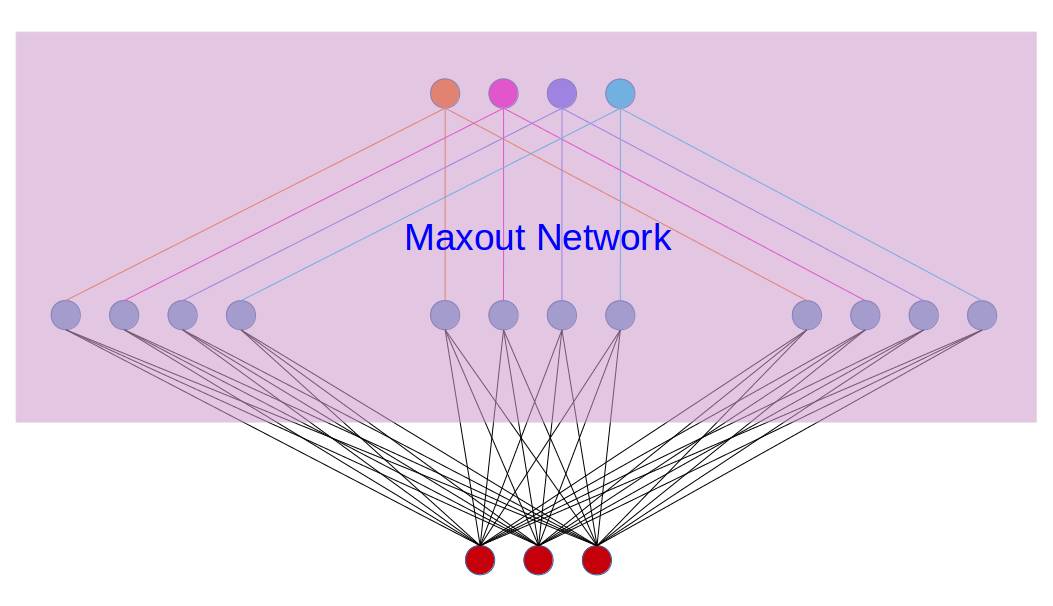
下面举例说明,如下图所示:
![]()
假设第i层有3个神经元(下),第i+1层有4个神经元(上),Maxout相当于在第i层和第i+1层之间新加了一层,现令k=3(中间三块),计算出三块各自的激活值(wiTx+bi),然后取三块中的最大值(max(w1Tx+b1,w2Tx+b2,...,wkTx+bk))作为第i层的输出。
优点:
- 具有ReLU的所有优点:线性、不饱和性
- 神经元不会死亡
缺点: