回溯法简述
回溯法是暴力法的升级版,我们可以将其解决问题的过程想象成一颗树,属于树型问题。
从根节点R开始,一步一步向下走,而每一步都会有多个(有限个)选择,对应多个子节点(A, B, C…)。若当前节点A匹配成功,则进入该节点的子节点(A-1, A-2, A-3…)继续匹配;若当前节点A匹配失败,则回到其父节点,继续匹配其他未曾匹配过的A的兄弟节点(B, C…),此过程称为回溯。
整个过程可以通过递归实现(深度优先遍历),也可以用栈实现。
算法题案例
矩阵中的路径
题目来源:剑指Offer
题目链接:牛客网-剑指Offer
题目描述:
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入该格子。 例如 a b c e s f c s a d e e 矩阵中包含一条字符串"bcced"的路径,但是矩阵中不包含"abcb"路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入该格子。
解题思路
1 | class Solution: |
运行结果
1 | solu = Solution() |
扩展
- 同时记录path所经过的路径坐标(self.path相关部分的代码)
1 | class Solution: |
- 运行结果
1 | solu = Solution() |
机器人的运动范围
题目来源:剑指Offer
题目链接:牛客网-剑指Offer
题目描述:
地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于k的格子。 例如,当k为18时,机器人能够进入方格(35,37),因为3+5+3+7 = 18。但是,它不能进入方格(35,38),因为3+5+3+8 = 19。请问该机器人能够达到多少个格子?
解题思路
1 | class Solution: |
注意:这道题没有进行 ‘self.visited[r][c] = 0’ 取消访问标记的操作,因为这道题问的是最多能到达的格子数,若改成能通过的最长路径,则需要取消标记。
运行结果
1 | solu = Solution() |
电话号码的字母组合
题目来源:Leetcode
题目链接:Leetcode-17
题目描述:
给定一个仅包含数字 2 - 9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
解题思路
深度优先遍历即可
1 | class Solution: |
运行结果
1 | solu = Solution() |
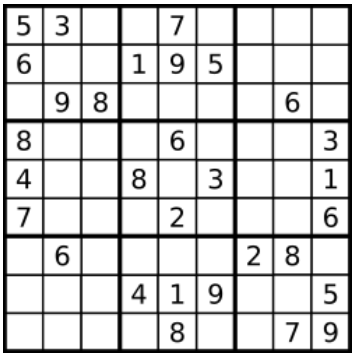
解数独
题目来源:Leetcode
题目链接:Leetcode-37
题目描述:
编写一个程序,通过已填充的空格来解决数独问题。
一个数独的解法需遵循如下规则:
1、数字 1-9 在每一行只能出现一次。
2、数字 1-9 在每一列只能出现一次。
3、数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
空白格用 ‘.’ 表示。
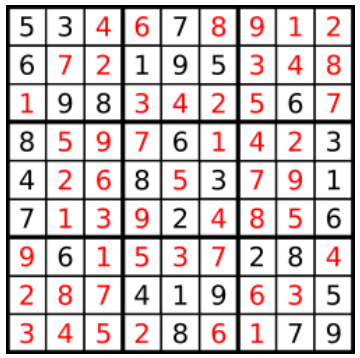
一个数独。
答案被标成红色。
解题思路
- 按照从左到右、从上到下的顺序遍历所有位置
- 从1~9选择合适的数字依次填入
- 若当前无合适的数字,则回溯
- 若已到达最后位置,则数独已解决
1 | class Solution(object): |
运行结果
1 | from pprint import pprint |
N皇后
题目来源:Leetcode
题目链接:Leetcode-51
题目描述:
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
上图为 8 皇后问题的一种解法。
给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
解题思路
N皇后问题实际上就是在NxN的数组中,对每一行找到一个位置,使得最终N个皇后不同行、不同列、不处于同一个主副对角线,我们最终要得到的结果实际上是一个list,其中第 i 个元素值 j 代表第 i 行的皇后处于第 j 列。
因此,我们只需要遍历每一行的N个值,遇到冲突时回溯即可。
对于所有的主对角线有 行号 + 列号 = 常数,对于所有的副对角线有 行号 - 列号 = 常数。
1 | class Solution(object): |
运行结果
1 | solu = Solution() |
优化
注意一个细节:一行只可能有一个皇后,一列也只可能有一个皇后。
这意味着没有必要考虑棋盘上所有的方格,只需要按行或列循环即可,这样也能省掉rowFlag和colFlag这两个标识,降低复杂度。
1 | class Solution(object): |