定义 1 矩阵的奇异值分解是指,将一个非零的 m ∗ n m * n m ∗ n A A A A ∈ R m ∗ n A \in {\rm R^{m * n}} A ∈ R m ∗ n
A = U Σ V T (1) A=U \Sigma V^T \tag{1}
A = U Σ V T ( 1 )
其中 U U U m m m 正交矩阵 ① ^① ① V V V n n n Σ \Sigma Σ m ∗ n m * n m ∗ n A A A 奇异值 (singular value),满足:
U U T = I V V T = I Σ = d i a g ( σ 1 , σ 2 , … , σ p ) σ 1 ≥ σ 2 ≥ ⋯ ≥ σ p ≥ 0 p = m i n ( m , n ) UU^T=I \\
VV^T=I \\
\Sigma=diag(\sigma_1, \sigma_2, \dots, \sigma_p) \\
\sigma_1 \ge \sigma_2 \ge \dots \ge \sigma_p \ge 0 \\
p=min(m, n)
U U T = I V V T = I Σ = d i a g ( σ 1 , σ 2 , … , σ p ) σ 1 ≥ σ 2 ≥ ⋯ ≥ σ p ≥ 0 p = m i n ( m , n )
U Σ V T U \Sigma V^T U Σ V T A A A 奇异值分解 (singular value decomposition, SVD ),σ i \sigma_i σ i A A A 奇异值 ,U U U V V V
① 正交矩阵 :正交矩阵 U U U U T U^T U T I I I U U T = I UU^T=I U U T = I
定理 1(奇异值分解基本定理) 若 A A A m ∗ n m * n m ∗ n A ∈ R m ∗ n A \in {\rm R}^{m * n} A ∈ R m ∗ n A A A
公式 (1) 给出的奇异值分解又称为矩阵的完全奇异值分解 (full singular value decomposition)。紧奇异值分解 是与原始矩阵等秩 的奇异值分解,截断奇异值分解 是比原始矩阵低秩 的奇异值分解。
例 1 设给定一个 5 ∗ 4 5 * 4 5 ∗ 4 A A A
A = [ 1 0 0 0 0 0 0 4 0 3 0 0 0 0 0 0 2 0 0 0 ] A=
\left[
\begin{matrix}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 4 \\
0 & 3 & 0 & 0 \\
0 & 0 & 0 & 0 \\
2 & 0 & 0 & 0 \\
\end{matrix}
\right]
A = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 2 0 0 3 0 0 0 0 0 0 0 0 4 0 0 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
它的完全奇异值分解 由三个矩阵的乘积 U Σ V T U \Sigma V^T U Σ V T
U = [ 0 0 0.2 0 0.8 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0.8 0 − 0.2 ] , Σ = [ 4 0 0 0 0 3 0 0 0 0 5 0 0 0 0 0 0 0 0 0 ] , V T = [ 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 ] U=
\left[
\begin{matrix}
0 & 0 & \sqrt{0.2} & 0 & \sqrt{0.8} \\
1 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 \\
0 & 0 & \sqrt{0.8} & 0 & -\sqrt{0.2} \\
\end{matrix}
\right],
\Sigma=
\left[
\begin{matrix}
4 & 0 & 0 & 0 \\
0 & 3 & 0 & 0 \\
0 & 0 & \sqrt{5} & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
\end{matrix}
\right],
V^T=
\left[
\begin{matrix}
0 & 0 & 0 & 1 \\
0 & 1 & 0 & 0 \\
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
\end{matrix}
\right]
U = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ 0 1 0 0 0 0 0 1 0 0 0 . 2 0 0 0 0 . 8 0 0 0 1 0 0 . 8 0 0 0 − 0 . 2 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ , Σ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ 4 0 0 0 0 0 3 0 0 0 0 0 5 0 0 0 0 0 0 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ , V T = ⎣ ⎢ ⎢ ⎡ 0 0 1 0 0 1 0 0 0 0 0 1 1 0 0 0 ⎦ ⎥ ⎥ ⎤
定义 2 设有 m ∗ n m * n m ∗ n A A A r a n k ( A ) = r rank(A)=r r a n k ( A ) = r r ≤ m i n ( m , n ) r \le min(m, n) r ≤ m i n ( m , n ) U r Σ r V r T U_r \Sigma_r V_r^T U r Σ r V r T A A A 紧奇异值分解 (compact singular value decomposition),即
A = U r Σ r V r T (2) A=U_r \Sigma_r V_r^T \tag{2}
A = U r Σ r V r T ( 2 )
其中 U r U_r U r m ∗ r m * r m ∗ r V r V_r V r n ∗ r n * r n ∗ r Σ r \Sigma_r Σ r r r r U r U_r U r U U U r r r V r V_r V r V V V r r r Σ r \Sigma_r Σ r Σ \Sigma Σ r r r Σ r \Sigma_r Σ r A A A 相等 。例 2 由例 1 给出的矩阵 A A A r = 3 r=3 r = 3 A A A 紧奇异值分解 是
U r = [ 0 0 0.2 1 0 0 0 1 0 0 0 0 0 0 0.8 ] , Σ r = [ 4 0 0 0 3 0 0 0 5 ] , V r T = [ 0 0 0 1 0 1 0 0 1 0 0 0 ] U_r=
\left[
\begin{matrix}
0 & 0 & \sqrt{0.2} \\
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 0 \\
0 & 0 & \sqrt{0.8} \\
\end{matrix}
\right],
\Sigma_r=
\left[
\begin{matrix}
4 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & \sqrt{5} \\
\end{matrix}
\right],
V_r^T=
\left[
\begin{matrix}
0 & 0 & 0 & 1 \\
0 & 1 & 0 & 0 \\
1 & 0 & 0 & 0 \\
\end{matrix}
\right]
U r = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ 0 1 0 0 0 0 0 1 0 0 0 . 2 0 0 0 0 . 8 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ , Σ r = ⎣ ⎡ 4 0 0 0 3 0 0 0 5 ⎦ ⎤ , V r T = ⎣ ⎡ 0 0 1 0 1 0 0 0 0 1 0 0 ⎦ ⎤
当我们只取最大的 k k k k < r k < r k < r r r r
实际应用中提到矩阵的奇异值分解时,通常指截断奇异值分解。
定义 3 设 A A A m ∗ n m * n m ∗ n r a n k ( A ) = r rank(A)=r r a n k ( A ) = r 0 < k < r 0 < k < r 0 < k < r U k Σ k V k T U_k \Sigma_k V_k^T U k Σ k V k T A A A 截断奇异值分解 (truncated singular value decomposition)
A ≈ U k Σ k V k T (3) A \approx U_k \Sigma_k V_k^T \tag{3}
A ≈ U k Σ k V k T ( 3 )
其中 U k U_k U k m ∗ k m * k m ∗ k V k V_k V k n ∗ k n * k n ∗ k Σ k \Sigma_k Σ k k k k U k U_k U k U U U k k k V k V_k V k V V V k k k Σ k \Sigma_k Σ k Σ \Sigma Σ k k k Σ k \Sigma_k Σ k A A A 低 。例 3 由例 1 给出的矩阵 A A A r = 3 r=3 r = 3 k = 2 k=2 k = 2 截断奇异值分解 是
U k = [ 0 0 1 0 0 1 0 0 0 0 ] , Σ k = [ 4 0 0 3 ] , V k T = [ 0 0 0 1 0 1 0 0 ] U_k=
\left[
\begin{matrix}
0 & 0 \\
1 & 0 \\
0 & 1 \\
0 & 0 \\
0 & 0 \\
\end{matrix}
\right],
\Sigma_k=
\left[
\begin{matrix}
4 & 0 \\
0 & 3 \\
\end{matrix}
\right],
V_k^T=
\left[
\begin{matrix}
0 & 0 & 0 & 1 \\
0 & 1 & 0 & 0 \\
\end{matrix}
\right]
U k = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ 0 1 0 0 0 0 0 1 0 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ , Σ k = [ 4 0 0 3 ] , V k T = [ 0 0 0 1 0 0 1 0 ]
此时
A k ≈ U k Σ k V k T = 外 积 展 开 式 σ 1 u 1 v 1 T + σ 2 u 2 v 2 T = [ 0 0 0 0 0 0 0 4 0 3 0 0 0 0 0 0 0 0 0 0 ] ( 红 色 字 体 处 的 数 字 与 A 相 比 已 改 变 ) A_k \approx U_k \Sigma_k V_k^T \overset{外积展开式}{=} \sigma_1u_1v_1^T+\sigma_2u_2v_2^T=
\left[
\begin{matrix}
\textcolor{red}{0} & 0 & 0 & 0 \\
0 & 0 & 0 & 4 \\
0 & 3 & 0 & 0 \\
0 & 0 & 0 & 0 \\
\textcolor{red}{0} & 0 & 0 & 0 \\
\end{matrix}
\right] (红色字体处的数字与A相比已改变)
A k ≈ U k Σ k V k T = 外 积 展 开 式 σ 1 u 1 v 1 T + σ 2 u 2 v 2 T = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 4 0 0 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ ( 红 色 字 体 处 的 数 字 与 A 相 比 已 改 变 )
在实际应用中,常常需要对矩阵的数据 进行压缩 ,将其近似表示,奇异值分解提供了一种方法。紧奇异值分解 是无损压缩 ,截断奇异值分解 是有损压缩 。
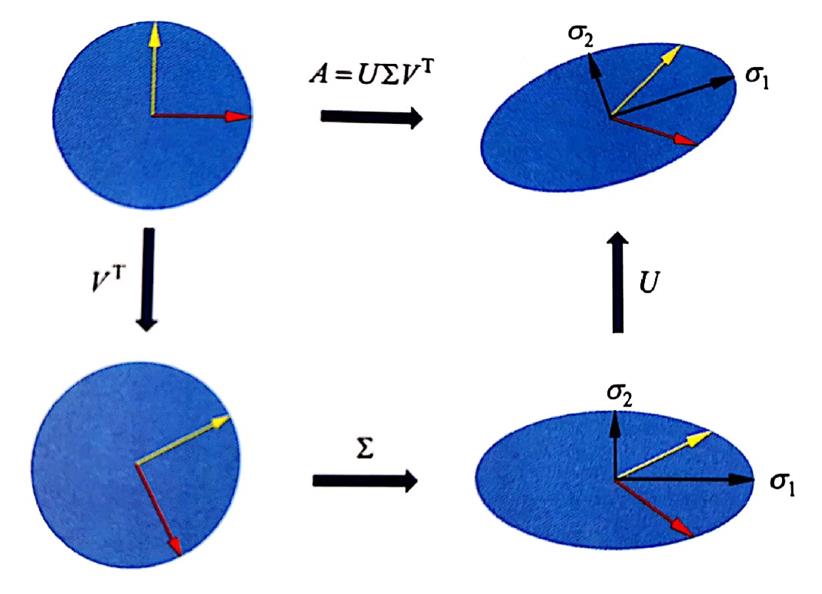
图源于李航的《统计学习方法》
上图给出了矩阵奇异值分解的直观的几何解释。原始空间的标准正交基(红色和黄色),经过坐标系的旋转变换 V T V^T V T 、坐标轴的缩放变换 Σ \Sigma Σ (黑色 σ 1 , σ 2 \sigma_1, \sigma_2 σ 1 , σ 2 旋转变换 U U U ,得到和经过线性变换 A A A 等价的结果。
( 1 ) 求 A T A 的 特 征 值 和 特 征 向 量 \textcolor{red}{(1) 求 A^TA 的特征值和特征向量} ( 1 ) 求 A T A 的 特 征 值 和 特 征 向 量 W = A T A W=A^TA W = A T A
( W − λ I ) x = 0 (W - \lambda I)x=0
( W − λ I ) x = 0
得到特征值 λ i \lambda_i λ i
λ 1 ≥ λ 2 ≥ ⋯ ≥ λ n ≥ 0 \lambda_1 \ge \lambda_2 \ge \dots \ge \lambda_n \ge 0
λ 1 ≥ λ 2 ≥ ⋯ ≥ λ n ≥ 0
将特征值 λ i \lambda_i λ i i = 1 , 2 , … , n i=1, 2, \dots, n i = 1 , 2 , … , n
( 2 ) 求 n 阶 正 交 矩 阵 V \textcolor{red}{(2) 求 n 阶正交矩阵 V} ( 2 ) 求 n 阶 正 交 矩 阵 V v 1 , v 2 , … , v n v_1, v_2, \dots, v_n v 1 , v 2 , … , v n n n n V V V
V = [ v 1 v 2 … v n ] V=\left[ \begin{matrix} v_1 & v_2 & \dots & v_n \end{matrix} \right]
V = [ v 1 v 2 … v n ]
( 3 ) 求 m ∗ n 对 角 矩 阵 Σ \textcolor{red}{(3) 求 m * n 对角矩阵 \Sigma} ( 3 ) 求 m ∗ n 对 角 矩 阵 Σ A A A
σ i = λ i , i=1, 2, … , n \sigma_i=\sqrt{\lambda_i} \text{, i=1, 2, \dots, n}
σ i = λ i , i=1, 2, … , n
构造 m ∗ n m * n m ∗ n Σ \Sigma Σ
Σ = d i a g ( σ 1 , σ 2 , … , σ n ) \Sigma=diag(\sigma_1, \sigma_2, \dots, \sigma_n)
Σ = d i a g ( σ 1 , σ 2 , … , σ n )
( 4 ) 求 m 阶 正 交 矩 阵 U \textcolor{red}{(4) 求 m 阶正交矩阵 U} ( 4 ) 求 m 阶 正 交 矩 阵 U A A A r r r
u j = 1 σ j A v j , j=1, 2, … , r u_j=\frac{1}{\sigma_j} Av_j \text{, j=1, 2, \dots, r}
u j = σ j 1 A v j , j=1, 2, … , r
得到
U 1 = [ u 1 u 2 … u r ] U_1=\left[ \begin{matrix} u_1 & u_2 & \dots & u_r \end{matrix} \right]
U 1 = [ u 1 u 2 … u r ]
求 A T A^T A T u r + 1 , u r + 2 , … , u m {u_{r+1}, u_{r+2}, \dots, u_m} u r + 1 , u r + 2 , … , u m
U 2 = [ u r + 1 u r + 2 … u m ] U_2=\left[ \begin{matrix} u_{r+1} & u_{r+2} & \dots & u_m \end{matrix} \right]
U 2 = [ u r + 1 u r + 2 … u m ]
并令
U = [ U 1 U 2 ] U=\left[ \begin{matrix} U_1 & U_2 \end{matrix} \right]
U = [ U 1 U 2 ]
( 5 ) 得 到 奇 异 值 分 解 \textcolor{red}{(5) 得到奇异值分解} ( 5 ) 得 到 奇 异 值 分 解
A = U Σ V T A=U \Sigma V^T
A = U Σ V T
例4 试求矩阵
A = [ 1 1 2 2 0 0 ] A=
\left[
\begin{matrix}
1 & 1 \\
2 & 2 \\
0 & 0 \\
\end{matrix}
\right]
A = ⎣ ⎡ 1 2 0 1 2 0 ⎦ ⎤
的奇异值分解。解 ( 1 ) 求 矩 阵 A T A 的 特 征 值 和 特 征 向 量 \textcolor{red}{(1) 求矩阵 A^TA 的特征值和特征向量} ( 1 ) 求 矩 阵 A T A 的 特 征 值 和 特 征 向 量 A T A A^TA A T A
A T A = [ 1 2 0 1 2 0 ] [ 1 1 2 2 0 0 ] = [ 5 5 5 5 ] A^TA=
\left[
\begin{matrix}
1 & 2 & 0 \\
1 & 2 & 0 \\
\end{matrix}
\right]
\left[
\begin{matrix}
1 & 1 \\
2 & 2 \\
0 & 0 \\
\end{matrix}
\right]
=
\left[
\begin{matrix}
5 & 5 \\
5 & 5 \\
\end{matrix}
\right]
A T A = [ 1 1 2 2 0 0 ] ⎣ ⎡ 1 2 0 1 2 0 ⎦ ⎤ = [ 5 5 5 5 ]
特征值 λ \lambda λ x x x
( A T A − λ I ) x = 0 (A^TA-\lambda I)x=0
( A T A − λ I ) x = 0
得到齐次线性方程组
{ ( 5 − λ ) x 1 + 5 x 2 = 0 5 x 1 + ( 5 − λ ) x 2 = 0 \begin{cases}
(5 - \lambda) &x_1 + 5 &x_2 &=0 \\
5 &x_1 + (5 - \lambda)&x_2 &=0 \\
\end{cases}
{ ( 5 − λ ) 5 x 1 + 5 x 1 + ( 5 − λ ) x 2 x 2 = 0 = 0
该方程组有非零解的充要条件是
∣ 5 − λ 5 5 5 − λ ∣ = 0 \begin{vmatrix}
5 - \lambda & 5 \\
5 & 5 - \lambda \\
\end{vmatrix}
=0
∣ ∣ ∣ ∣ 5 − λ 5 5 5 − λ ∣ ∣ ∣ ∣ = 0
即
λ 2 − 10 λ = 0 \lambda^2-10\lambda=0
λ 2 − 1 0 λ = 0
解此方程,得到矩阵 A T A A^TA A T A
{ λ 1 = 10 λ 2 = 0 \begin{cases}
\lambda_1=10 \\
\lambda_2=0 \\
\end{cases}
{ λ 1 = 1 0 λ 2 = 0
将特征值 λ 1 = 10 \lambda_1=10 λ 1 = 1 0 x 1 − x 2 = 0 x_1-x_2=0 x 1 − x 2 = 0
v 1 = [ 1 1 ] = 单 位 化 [ 1 2 1 2 ] v_1=
\left[
\begin{matrix}
1 \\
1 \\
\end{matrix}
\right]
\overset{单位化}{=}
\left[
\begin{matrix}
\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} \\
\end{matrix}
\right]
v 1 = [ 1 1 ] = 单 位 化 [ 2 1 2 1 ]
同样将特征值 λ 2 = 0 \lambda_2=0 λ 2 = 0 x 1 + x 2 = 0 x_1+x_2=0 x 1 + x 2 = 0
v 2 = [ 1 − 1 ] = 单 位 化 [ 1 2 − 1 2 ] v_2=
\left[
\begin{matrix}
1 \\
-1 \\
\end{matrix}
\right]
\overset{单位化}{=}
\left[
\begin{matrix}
\frac{1}{\sqrt{2}} \\
-\frac{1}{\sqrt{2}} \\
\end{matrix}
\right]
v 2 = [ 1 − 1 ] = 单 位 化 [ 2 1 − 2 1 ]
( 2 ) 求 正 交 矩 阵 V \textcolor{red}{(2) 求正交矩阵 V} ( 2 ) 求 正 交 矩 阵 V V V V
V = [ v 1 v 2 ] = [ 1 2 1 2 1 2 − 1 2 ] V=
\left[
\begin{matrix}
v_1 & v_2 \\
\end{matrix}
\right]
=
\left[
\begin{matrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\end{matrix}
\right]
V = [ v 1 v 2 ] = [ 2 1 2 1 2 1 − 2 1 ]
( 3 ) 求 对 角 矩 阵 Σ \textcolor{red}{(3) 求对角矩阵 \Sigma} ( 3 ) 求 对 角 矩 阵 Σ σ 1 = λ 1 = 10 \sigma_1=\sqrt{\lambda_1}=\sqrt{10} σ 1 = λ 1 = 1 0 σ 2 = 0 \sigma_2=0 σ 2 = 0 Σ \Sigma Σ
Σ = [ σ 1 0 0 σ 2 0 0 ] = [ 10 0 0 0 0 0 ] \Sigma=
\left[
\begin{matrix}
\sigma_1 & 0 \\
0 & \sigma_2 \\
0 & 0 \\
\end{matrix}
\right]
=
\left[
\begin{matrix}
\sqrt{10} & 0 \\
0 & 0 \\
0 & 0 \\
\end{matrix}
\right]
Σ = ⎣ ⎡ σ 1 0 0 0 σ 2 0 ⎦ ⎤ = ⎣ ⎡ 1 0 0 0 0 0 0 ⎦ ⎤
注意:Σ \Sigma Σ Σ \Sigma Σ U U U V V V
( 4 ) 求 正 交 矩 阵 U \textcolor{red}{(4) 求正交矩阵 U} ( 4 ) 求 正 交 矩 阵 U A A A u 1 u_1 u 1
u 1 = 1 σ 1 A v 1 = 1 10 [ 1 1 2 2 0 0 ] [ 1 2 1 2 ] = [ 1 5 2 5 0 ] u_1=\frac{1}{\sigma_1}Av_1=\frac{1}{\sqrt{10}}
\left[
\begin{matrix}
1 & 1 \\
2 & 2 \\
0 & 0 \\
\end{matrix}
\right]
\left[
\begin{matrix}
\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} \\
\end{matrix}
\right]
=
\left[
\begin{matrix}
\frac{1}{\sqrt{5}} \\
\frac{2}{\sqrt{5}} \\
0 \\
\end{matrix}
\right]
u 1 = σ 1 1 A v 1 = 1 0 1 ⎣ ⎡ 1 2 0 1 2 0 ⎦ ⎤ [ 2 1 2 1 ] = ⎣ ⎡ 5 1 5 2 0 ⎦ ⎤
列向量 u 2 , u 3 u_2, u_3 u 2 , u 3 A T A^T A T N ( A T ) N(A^T) N ( A T )
A T x = [ 1 2 0 1 2 0 ] [ x 1 x 2 x 3 ] = [ 0 0 ] A^Tx=
\left[
\begin{matrix}
1 & 2 & 0 \\
1 & 2 & 0 \\
\end{matrix}
\right]
\left[
\begin{matrix}
x_1 \\
x_2 \\
x_3 \\
\end{matrix}
\right]
=
\left[
\begin{matrix}
0 \\
0 \\
\end{matrix}
\right]
A T x = [ 1 1 2 2 0 0 ] ⎣ ⎡ x 1 x 2 x 3 ⎦ ⎤ = [ 0 0 ]
得 x 1 + 2 x 2 + 0 x 3 = 0 x_1+2x_2+0x_3 = 0 x 1 + 2 x 2 + 0 x 3 = 0 x 1 = − 2 x 2 − 0 x 3 x_1 = -2x_2-0x_3 x 1 = − 2 x 2 − 0 x 3 x 3 x_3 x 3 x 2 x_2 x 2 x 1 x_1 x 1 ( x 2 , x 3 ) (x_2, x_3) ( x 2 , x 3 ) ( 1 , 0 ) (1, 0) ( 1 , 0 ) ( 0 , 1 ) (0, 1) ( 0 , 1 )
( − 2 , 1 , 0 ) T , ( 0 , 0 , 1 ) T (-2, 1, 0)^T, (0, 0, 1)^T
( − 2 , 1 , 0 ) T , ( 0 , 0 , 1 ) T
标准化后,得到标准正交基为
{ u 2 = ( − 2 5 , 1 5 , 0 ) T u 3 = ( 0 , 0 , 1 ) T \begin{cases}
u_2=(-\frac{2}{\sqrt{5}}, \frac{1}{\sqrt{5}}, 0)^T \\
u_3=(0, 0, 1)^T \\
\end{cases}
{ u 2 = ( − 5 2 , 5 1 , 0 ) T u 3 = ( 0 , 0 , 1 ) T
构造正交矩阵 U U U
U = [ 1 5 − 2 5 0 2 5 1 5 0 0 0 1 ] U=
\left[
\begin{matrix}
\frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{5}} & 0 \\
\frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}} & 0 \\
0 & 0 & 1 \\
\end{matrix}
\right]
U = ⎣ ⎡ 5 1 5 2 0 − 5 2 5 1 0 0 0 1 ⎦ ⎤
( 5 ) 矩 阵 A 的 奇 异 值 分 解 \textcolor{red}{(5) 矩阵 A 的奇异值分解} ( 5 ) 矩 阵 A 的 奇 异 值 分 解
A = U Σ V T = [ 1 5 − 2 5 0 2 5 1 5 0 0 0 1 ] [ 10 0 0 0 0 0 ] [ 1 2 1 2 1 2 − 1 2 ] A=U \Sigma V^T=
\left[
\begin{matrix}
\frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{5}} & 0 \\
\frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}} & 0 \\
0 & 0 & 1 \\
\end{matrix}
\right]
\left[
\begin{matrix}
\sqrt{10} & 0 \\
0 & 0 \\
0 & 0 \\
\end{matrix}
\right]
\left[
\begin{matrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\end{matrix}
\right]
A = U Σ V T = ⎣ ⎡ 5 1 5 2 0 − 5 2 5 1 0 0 0 1 ⎦ ⎤ ⎣ ⎡ 1 0 0 0 0 0 0 ⎦ ⎤ [ 2 1 2 1 2 1 − 2 1 ]
( 1 ) 对 A T A 做 特 征 值 分 解 \textcolor{red}{(1) 对 A^TA 做特征值分解} ( 1 ) 对 A T A 做 特 征 值 分 解 A T A A^TA A T A
A T A = [ 5 5 5 5 ] A^TA=
\left[
\begin{matrix}
5 & 5 \\
5 & 5 \\
\end{matrix}
\right]
A T A = [ 5 5 5 5 ]
得到 A T A A^TA A T A λ \lambda λ x x x
{ λ 1 = 10 , x 1 = [ 1 2 1 2 ] λ 2 = 0 , x 2 = [ 1 2 − 1 2 ] , \begin{cases}
\lambda_1=10, x_1=\left[ \begin{matrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{matrix} \right] \\
\lambda_2=0, x_2=\left[ \begin{matrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \end{matrix} \right] \\
\end{cases},
⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ λ 1 = 1 0 , x 1 = [ 2 1 2 1 ] λ 2 = 0 , x 2 = [ 2 1 − 2 1 ] ,
( 2 ) 对 A A T 做 特 征 值 分 解 \textcolor{red}{(2) 对 AA^T 做特征值分解} ( 2 ) 对 A A T 做 特 征 值 分 解 A A T AA^T A A T
A A T = [ 2 4 0 4 8 0 0 0 0 ] AA^T=
\left[
\begin{matrix}
2 & 4 & 0 \\
4 & 8 & 0 \\
0 & 0 & 0 \\
\end{matrix}
\right]
A A T = ⎣ ⎡ 2 4 0 4 8 0 0 0 0 ⎦ ⎤
得到 A A T AA^T A A T λ \lambda λ x x x
{ λ 1 = 10 , x 1 = [ 1 5 2 5 0 ] λ 2 = 0 , x 2 = [ − 2 5 1 5 0 ] λ 3 = 0 , x 3 = [ 0 0 1 ] , \begin{cases}
\lambda_1=10, x_1=\left[ \begin{matrix} \frac{1}{\sqrt{5}} \\ \frac{2}{\sqrt{5}} \\ 0 \end{matrix} \right] \\
\lambda_2=0, x_2=\left[ \begin{matrix} -\frac{2}{\sqrt{5}} \\ \frac{1}{\sqrt{5}} \\ 0 \end{matrix} \right] \\
\lambda_3=0, x_3=\left[ \begin{matrix} 0 \\ 0 \\ 1 \end{matrix} \right] \\
\end{cases},
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ λ 1 = 1 0 , x 1 = ⎣ ⎡ 5 1 5 2 0 ⎦ ⎤ λ 2 = 0 , x 2 = ⎣ ⎡ − 5 2 5 1 0 ⎦ ⎤ λ 3 = 0 , x 3 = ⎣ ⎡ 0 0 1 ⎦ ⎤ ,
( 3 ) A T A 的 特 征 向 量 构 造 正 交 矩 阵 V \textcolor{red}{(3) A^TA 的特征向量构造正交矩阵 V} ( 3 ) A T A 的 特 征 向 量 构 造 正 交 矩 阵 V
V = [ 1 2 1 2 1 2 − 1 2 ] V=
\left[
\begin{matrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\end{matrix}
\right]
V = [ 2 1 2 1 2 1 − 2 1 ]
( 4 ) A A T 的 特 征 向 量 构 造 正 交 矩 阵 U \textcolor{red}{(4) AA^T 的特征向量构造正交矩阵 U} ( 4 ) A A T 的 特 征 向 量 构 造 正 交 矩 阵 U
U = [ 1 5 − 2 5 0 2 5 1 5 0 0 0 1 ] U=
\left[
\begin{matrix}
\frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{5}} & 0 \\
\frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}} & 0 \\
0 & 0 & 1 \\
\end{matrix}
\right]
U = ⎣ ⎡ 5 1 5 2 0 − 5 2 5 1 0 0 0 1 ⎦ ⎤
( 5 ) A T A 或 A A T 的 特 征 值 构 造 对 角 矩 阵 Σ \textcolor{red}{(5) A^TA 或 AA^T 的特征值构造对角矩阵 \Sigma} ( 5 ) A T A 或 A A T 的 特 征 值 构 造 对 角 矩 阵 Σ
Σ = [ 10 0 0 0 0 0 ] \Sigma=
\left[
\begin{matrix}
\sqrt{10} & 0 \\
0 & 0 \\
0 & 0 \\
\end{matrix}
\right]
Σ = ⎣ ⎡ 1 0 0 0 0 0 0 ⎦ ⎤
( 6 ) 矩 阵 A 的 奇 异 值 分 解 \textcolor{red}{(6) 矩阵 A 的奇异值分解} ( 6 ) 矩 阵 A 的 奇 异 值 分 解
A = U Σ V T = [ 1 5 − 2 5 0 2 5 1 5 0 0 0 1 ] [ 10 0 0 0 0 0 ] [ 1 2 1 2 1 2 − 1 2 ] A=U \Sigma V^T=
\left[
\begin{matrix}
\frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{5}} & 0 \\
\frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}} & 0 \\
0 & 0 & 1 \\
\end{matrix}
\right]
\left[
\begin{matrix}
\sqrt{10} & 0 \\
0 & 0 \\
0 & 0 \\
\end{matrix}
\right]
\left[
\begin{matrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\end{matrix}
\right]
A = U Σ V T = ⎣ ⎡ 5 1 5 2 0 − 5 2 5 1 0 0 0 1 ⎦ ⎤ ⎣ ⎡ 1 0 0 0 0 0 0 ⎦ ⎤ [ 2 1 2 1 2 1 − 2 1 ]