奇异值分解——《统计学习方法》第15章学习笔记

奇异值分解的定义

  定义 1 矩阵的奇异值分解是指，将一个非零的 $m * n$ 实矩阵$A$，$A \in {\rm R^{m * n}}$，表示为以下三个实矩阵乘积形式的运算，即进行矩阵的因子分解：

$A=U \Sigma V^T \tag{1}$

  其中 $U$ 是 $m$ 阶正交矩阵$^①$（orthogonal matrix），$V$ 是 $n$ 阶正交矩阵，$\Sigma$ 是由降序排列的非负的对角线元素组成的 $m * n$ 矩形对角矩阵（rectangular diagonal matrix），其对角线上的非负元素即为矩阵 $A$ 降序排列的奇异值（singular value），满足：

$UU^T=I \\ VV^T=I \\ \Sigma=diag(\sigma_1, \sigma_2, \dots, \sigma_p) \\ \sigma_1 \ge \sigma_2 \ge \dots \ge \sigma_p \ge 0 \\ p=min(m, n)$

  $U \Sigma V^T$ 称为矩阵 $A$ 的奇异值分解（singular value decomposition, SVD），$\sigma_i$ 称为矩阵 $A$ 的奇异值，$U$ 的列向量称为左奇异向量（left singular vector），$V$ 的列向量称为右奇异向量（right singular vector）。

① 正交矩阵：正交矩阵 $U$ 和其转置矩阵 $U^T$ 相乘的结果是单位矩阵 $I$ 。（$UU^T=I$）

  定理 1（奇异值分解基本定理） 若 $A$ 为一 $m * n$ 实矩阵，$A \in {\rm R}^{m * n}$，则 $A$ 的奇异值分解存在。

紧奇异值分解和截断奇异值分解

  公式 (1) 给出的奇异值分解又称为矩阵的完全奇异值分解（full singular value decomposition）。
  实际常用的是奇异值分解的紧凑形式和截断形式。紧奇异值分解是与原始矩阵等秩的奇异值分解，截断奇异值分解是比原始矩阵低秩的奇异值分解。

  例 1  设给定一个 $5 * 4$ 矩阵 $A$：

$A= \left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 2 & 0 & 0 & 0 \\ \end{matrix} \right]$

  它的完全奇异值分解由三个矩阵的乘积 $U \Sigma V^T$ 给出：

$U= \left[ \begin{matrix} 0 & 0 & \sqrt{0.2} & 0 & \sqrt{0.8} \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & \sqrt{0.8} & 0 & -\sqrt{0.2} \\ \end{matrix} \right], \Sigma= \left[ \begin{matrix} 4 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & \sqrt{5} & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{matrix} \right], V^T= \left[ \begin{matrix} 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{matrix} \right]$

紧奇异值分解

  定义 2 设有 $m * n$ 实矩阵 $A$ ，其秩为 $rank(A)=r$ ，$r \le min(m, n)$，则称$U_r \Sigma_r V_r^T$ 为 $A$ 的紧奇异值分解（compact singular value decomposition），即

$A=U_r \Sigma_r V_r^T \tag{2}$

  其中 $U_r$ 是 $m * r$ 矩阵，$V_r$ 是 $n * r$ 矩阵，$\Sigma_r$ 是 $r$ 阶对角矩阵。
  矩阵 $U_r$ 由完全奇异值分解中 $U$ 的前 $r$ 列、矩阵 $V_r$ 由 $V$ 的前 $r$ 列、矩阵 $\Sigma_r$ 由 $\Sigma$ 的前 $r$ 个对角线元素得到。
  紧奇异值分解的对角矩阵 $\Sigma_r$ 的秩与原始矩阵 $A$ 的秩相等。
  例 2  由例 1 给出的矩阵 $A$，它的秩 $r=3$，得到 $A$ 的紧奇异值分解是

$U_r= \left[ \begin{matrix} 0 & 0 & \sqrt{0.2} \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & \sqrt{0.8} \\ \end{matrix} \right], \Sigma_r= \left[ \begin{matrix} 4 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & \sqrt{5} \\ \end{matrix} \right], V_r^T= \left[ \begin{matrix} 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ \end{matrix} \right]$

截断奇异值分解

  当我们只取最大的 $k$ 个奇异值（$k < r$，$r$ 为矩阵的秩）对应的部分，就得到矩阵的截断奇异值分解。

实际应用中提到矩阵的奇异值分解时，通常指截断奇异值分解。

  定义 3 设 $A$ 为 $m * n$ 实矩阵，其秩 $rank(A)=r$，且 $0 < k < r$，则称 $U_k \Sigma_k V_k^T$ 为矩阵 $A$ 的截断奇异值分解（truncated singular value decomposition）

$A \approx U_k \Sigma_k V_k^T \tag{3}$

  其中 $U_k$ 是 $m * k$ 矩阵，$V_k$ 是 $n * k$ 矩阵，$\Sigma_k$ 是 $k$ 阶对角矩阵。
  矩阵 $U_k$ 由完全奇异值分解中 $U$ 的前 $k$ 列、矩阵 $V_k$ 由 $V$ 的前 $k$ 列、矩阵 $\Sigma_k$ 由 $\Sigma$ 的前 $k$ 个对角线元素得到。
  对角矩阵 $\Sigma_k$ 的秩比原始矩阵 $A$ 的秩低。
  例 3  由例 1 给出的矩阵 $A$，它的秩 $r=3$，若取 $k=2$，则其截断奇异值分解是

$U_k= \left[ \begin{matrix} 0 & 0 \\ 1 & 0 \\ 0 & 1 \\ 0 & 0 \\ 0 & 0 \\ \end{matrix} \right], \Sigma_k= \left[ \begin{matrix} 4 & 0 \\ 0 & 3 \\ \end{matrix} \right], V_k^T= \left[ \begin{matrix} 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ \end{matrix} \right]$

此时

$A_k \approx U_k \Sigma_k V_k^T \overset{外积展开式}{=} \sigma_1u_1v_1^T+\sigma_2u_2v_2^T= \left[ \begin{matrix} \textcolor{red}{0} & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \textcolor{red}{0} & 0 & 0 & 0 \\ \end{matrix} \right] (红色字体处的数字与A相比已改变)$

在实际应用中，常常需要对矩阵的数据进行压缩，将其近似表示，奇异值分解提供了一种方法。
紧奇异值分解是无损压缩，截断奇异值分解是有损压缩。

几何解释

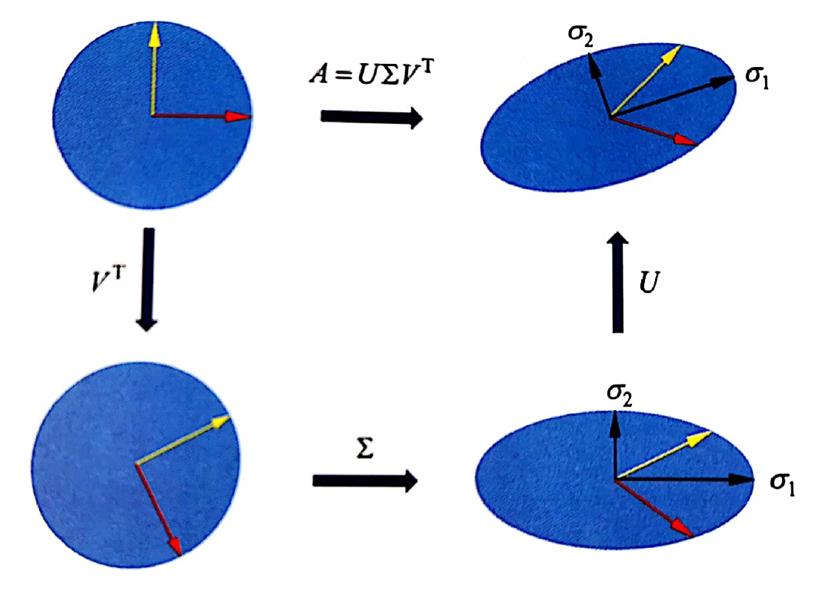
图源于李航的《统计学习方法》

  上图给出了矩阵奇异值分解的直观的几何解释。原始空间的标准正交基（红色和黄色），经过坐标系的旋转变换 $V^T$、坐标轴的缩放变换 $\Sigma$ （黑色 $\sigma_1, \sigma_2$）、坐标系的旋转变换 $U$，得到和经过线性变换 $A$ 等价的结果。

奇异值分解的计算

解法一

  $\textcolor{red}{(1) 求 A^TA 的特征值和特征向量}$
  计算对称矩阵 $W=A^TA$。
  求解特征方程

$(W - \lambda I)x=0$

得到特征值 $\lambda_i$，并将特征值由大到小排列

$\lambda_1 \ge \lambda_2 \ge \dots \ge \lambda_n \ge 0$

将特征值 $\lambda_i$（$i=1, 2, \dots, n$）代入特征方程求得对应的特征向量。

  $\textcolor{red}{(2) 求 n 阶正交矩阵 V}$
  将特征向量单位化，得到单位特征向量 $v_1, v_2, \dots, v_n$，构成 $n$ 阶正交矩阵 $V$:

$V=\left[ \begin{matrix} v_1 & v_2 & \dots & v_n \end{matrix} \right]$

  $\textcolor{red}{(3) 求 m * n 对角矩阵 \Sigma}$
  计算 $A$ 的奇异值

$\sigma_i=\sqrt{\lambda_i} \text{, i=1, 2, \dots, n}$

构造 $m * n$ 矩形对角矩阵 $\Sigma$，主对角线元素是奇异值，其余元素是零，

$\Sigma=diag(\sigma_1, \sigma_2, \dots, \sigma_n)$

  $\textcolor{red}{(4) 求 m 阶正交矩阵 U}$
  对 $A$ 的前 $r$ 个正奇异值，令

$u_j=\frac{1}{\sigma_j} Av_j \text{, j=1, 2, \dots, r}$

得到

$U_1=\left[ \begin{matrix} u_1 & u_2 & \dots & u_r \end{matrix} \right]$

  求 $A^T$ 的零空间的一组标准正交基 ${u_{r+1}, u_{r+2}, \dots, u_m}$，令

$U_2=\left[ \begin{matrix} u_{r+1} & u_{r+2} & \dots & u_m \end{matrix} \right]$

并令

$U=\left[ \begin{matrix} U_1 & U_2 \end{matrix} \right]$

  $\textcolor{red}{(5) 得到奇异值分解}$

$A=U \Sigma V^T$

例题讲解

  例4 试求矩阵

$A= \left[ \begin{matrix} 1 & 1 \\ 2 & 2 \\ 0 & 0 \\ \end{matrix} \right]$

的奇异值分解。
  解 $\textcolor{red}{(1) 求矩阵 A^TA 的特征值和特征向量}$
  求对称矩阵 $A^TA$

$A^TA= \left[ \begin{matrix} 1 & 2 & 0 \\ 1 & 2 & 0 \\ \end{matrix} \right] \left[ \begin{matrix} 1 & 1 \\ 2 & 2 \\ 0 & 0 \\ \end{matrix} \right] = \left[ \begin{matrix} 5 & 5 \\ 5 & 5 \\ \end{matrix} \right]$

  特征值 $\lambda$ 和特征向量 $x$ 满足特征方程

$(A^TA-\lambda I)x=0$

得到齐次线性方程组

$\begin{cases} (5 - \lambda) &x_1 + 5 &x_2 &=0 \\ 5 &x_1 + (5 - \lambda)&x_2 &=0 \\ \end{cases}$

该方程组有非零解的充要条件是

$\begin{vmatrix} 5 - \lambda & 5 \\ 5 & 5 - \lambda \\ \end{vmatrix} =0$

即

$\lambda^2-10\lambda=0$

解此方程，得到矩阵 $A^TA$ 的特征值

$\begin{cases} \lambda_1=10 \\ \lambda_2=0 \\ \end{cases}$

  将特征值 $\lambda_1=10$ 代入线性方程组，得 $x_1-x_2=0$ ，可得到对应的单位特征向量

$v_1= \left[ \begin{matrix} 1 \\ 1 \\ \end{matrix} \right] \overset{单位化}{=} \left[ \begin{matrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ \end{matrix} \right]$

同样将特征值 $\lambda_2=0$ 代入，得 $x_1+x_2=0$ ，对应的单位特征向量

$v_2= \left[ \begin{matrix} 1 \\ -1 \\ \end{matrix} \right] \overset{单位化}{=} \left[ \begin{matrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \\ \end{matrix} \right]$

  $\textcolor{red}{(2) 求正交矩阵 V}$
  构造正交矩阵 $V$

$V= \left[ \begin{matrix} v_1 & v_2 \\ \end{matrix} \right] = \left[ \begin{matrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \end{matrix} \right]$

  $\textcolor{red}{(3) 求对角矩阵 \Sigma}$
  奇异值为 $\sigma_1=\sqrt{\lambda_1}=\sqrt{10}$ 和 $\sigma_2=0$。构造对角矩阵 $\Sigma$

$\Sigma= \left[ \begin{matrix} \sigma_1 & 0 \\ 0 & \sigma_2 \\ 0 & 0 \\ \end{matrix} \right] = \left[ \begin{matrix} \sqrt{10} & 0 \\ 0 & 0 \\ 0 & 0 \\ \end{matrix} \right]$

注意：$\Sigma$ 中要加上零行向量（最后的一行0），使得 $\Sigma$ 能够与 $U$ ，$V$ 进行矩阵乘法运算。

  $\textcolor{red}{(4) 求正交矩阵 U}$
  基于 $A$ 的正奇异值计算得到列向量 $u_1$

$u_1=\frac{1}{\sigma_1}Av_1=\frac{1}{\sqrt{10}} \left[ \begin{matrix} 1 & 1 \\ 2 & 2 \\ 0 & 0 \\ \end{matrix} \right] \left[ \begin{matrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ \end{matrix} \right] = \left[ \begin{matrix} \frac{1}{\sqrt{5}} \\ \frac{2}{\sqrt{5}} \\ 0 \\ \end{matrix} \right]$

  列向量 $u_2, u_3$ 是 $A^T$ 的零空间 $N(A^T)$ 的一组标准正交基。为此，求解以下线性方程组

$A^Tx= \left[ \begin{matrix} 1 & 2 & 0 \\ 1 & 2 & 0 \\ \end{matrix} \right] \left[ \begin{matrix} x_1 \\ x_2 \\ x_3 \\ \end{matrix} \right] = \left[ \begin{matrix} 0 \\ 0 \\ \end{matrix} \right]$

得 $x_1+2x_2+0x_3 = 0$
即 $x_1 = -2x_2-0x_3$
可见 $x_3$ 可以取任意值，$x_2$ 的改变会影响到 $x_1$，因此我们分别取 $(x_2, x_3)$ 为 $(1, 0)$ 和 $(0, 1)$，得到一组基为

$(-2, 1, 0)^T, (0, 0, 1)^T$

标准化后，得到标准正交基为

$\begin{cases} u_2=(-\frac{2}{\sqrt{5}}, \frac{1}{\sqrt{5}}, 0)^T \\ u_3=(0, 0, 1)^T \\ \end{cases}$

构造正交矩阵 $U$

$U= \left[ \begin{matrix} \frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{5}} & 0 \\ \frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}} & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right]$

  $\textcolor{red}{(5) 矩阵 A 的奇异值分解}$

$A=U \Sigma V^T= \left[ \begin{matrix} \frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{5}} & 0 \\ \frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}} & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right] \left[ \begin{matrix} \sqrt{10} & 0 \\ 0 & 0 \\ 0 & 0 \\ \end{matrix} \right] \left[ \begin{matrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \end{matrix} \right]$

解法二

  $\textcolor{red}{(1) 对 A^TA 做特征值分解}$
  计算 $A^TA$

$A^TA= \left[ \begin{matrix} 5 & 5 \\ 5 & 5 \\ \end{matrix} \right]$

  得到 $A^TA$ 的特征值 $\lambda$ 和特征向量 $x$

$\begin{cases} \lambda_1=10, x_1=\left[ \begin{matrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{matrix} \right] \\ \lambda_2=0, x_2=\left[ \begin{matrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \end{matrix} \right] \\ \end{cases},$

  $\textcolor{red}{(2) 对 AA^T 做特征值分解}$
  计算 $AA^T$

$AA^T= \left[ \begin{matrix} 2 & 4 & 0 \\ 4 & 8 & 0 \\ 0 & 0 & 0 \\ \end{matrix} \right]$

  得到 $AA^T$ 的特征值 $\lambda$ 和特征向量 $x$

$\begin{cases} \lambda_1=10, x_1=\left[ \begin{matrix} \frac{1}{\sqrt{5}} \\ \frac{2}{\sqrt{5}} \\ 0 \end{matrix} \right] \\ \lambda_2=0, x_2=\left[ \begin{matrix} -\frac{2}{\sqrt{5}} \\ \frac{1}{\sqrt{5}} \\ 0 \end{matrix} \right] \\ \lambda_3=0, x_3=\left[ \begin{matrix} 0 \\ 0 \\ 1 \end{matrix} \right] \\ \end{cases},$

  $\textcolor{red}{(3) A^TA 的特征向量构造正交矩阵 V}$

$V= \left[ \begin{matrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \end{matrix} \right]$

  $\textcolor{red}{(4) AA^T 的特征向量构造正交矩阵 U}$

$U= \left[ \begin{matrix} \frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{5}} & 0 \\ \frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}} & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right]$

  $\textcolor{red}{(5) A^TA 或 AA^T 的特征值构造对角矩阵 \Sigma}$

$\Sigma= \left[ \begin{matrix} \sqrt{10} & 0 \\ 0 & 0 \\ 0 & 0 \\ \end{matrix} \right]$

  $\textcolor{red}{(6) 矩阵 A 的奇异值分解}$

$A=U \Sigma V^T= \left[ \begin{matrix} \frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{5}} & 0 \\ \frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}} & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right] \left[ \begin{matrix} \sqrt{10} & 0 \\ 0 & 0 \\ 0 & 0 \\ \end{matrix} \right] \left[ \begin{matrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \end{matrix} \right]$