牛顿迭代法的介绍
牛顿迭代法(Newton’s method)又称为牛顿-拉弗森方法(Newton-Raphson method),是一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式,因此求其精确根非常困难,甚至不可能,因此,寻找方程的近似根就显得特别重要。
牛顿迭代公式的推导方法一
牛顿法使用函数f(x)的泰勒展开式的前面几项来寻找方程f(x)=0的根。对于一个函数f(x),它的泰勒展开式如下:
f(x)=f(x0)+f′(x0)(x−x0)+21f′′(x0)(x−x0)2+⋯+n!1fn(x0)(x−x0)n,
我们使用其前两项来近似表示这个函数,即用θ(x)代替f(x):
θ(x)=f(x0)+f′(x0)(x−x0),
令θ(x)=0,则x=x0−f′(x0)f(x0),所以,牛顿法的迭代公式就是:
xn+1=xn−f′(xn)f(xn).
牛顿迭代公式的推导方法二
- 有同学可能要说了,这个泰勒展开式我记不住咋办?有没有别的方法呢?
- 别慌,当然有 ————
设r是函数f(x)=0的根,我们不知道它是多少,现在需要用牛顿法近似求解r。
1、我们首先取一个r的初始近似值x0,过点(x0,f(x0))作函数f(x)的切线L1,设
L1:y=kx+b,
其中斜率k就是函数f(x)在x0点处的导数,即:
k=f′(x0),
将点(x0,f(x0))代入L1可得:
b=f(x0)−f′(x0)x0,
因此切线L1:
y=f(x0)+f′(x0)(x−x0),
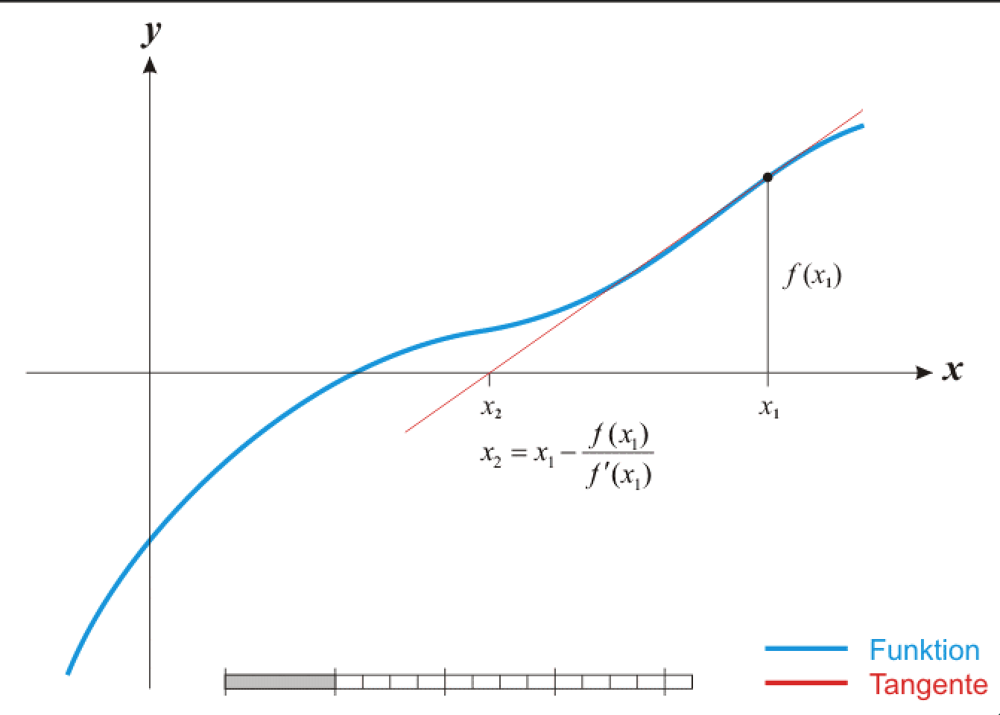
2、接着我们可以求出L1与x轴的交点的横坐标x1,令y=0即可得:
x1=x0−f′(x0)f(x0),
我们称x1为r的一次近似值。
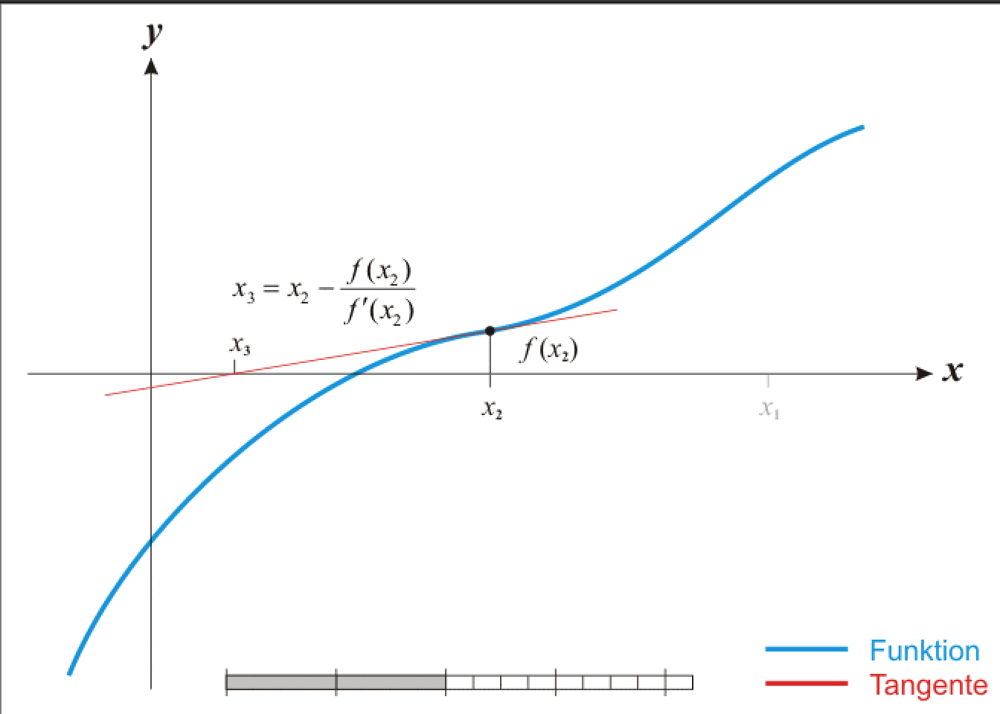
3、同理,我们过点(x1,f(x1))作函数f(x)的切线L2,并求该切线与x轴的交点的横坐标:
x2=x1−f′(x1)f(x1),
称x2为r的二次近似值。
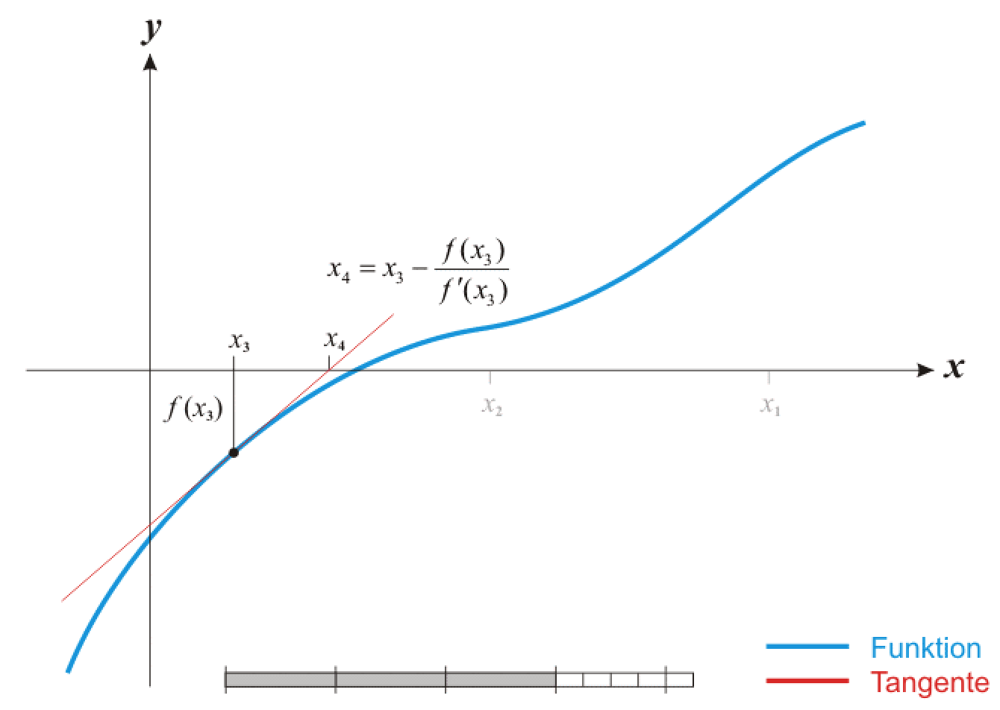
4、重复以上过程,可得到r的n+1次近似值,也就是牛顿迭代公式:
xn+1=xn−f′(xn)f(xn).
牛顿迭代公式的形象理解
- ①、随机选一个初始值x1,进行一次迭代,寻找到x2
![]()
- ②、x2⇒x3
![]()
- ③、x3⇒x4
![]()
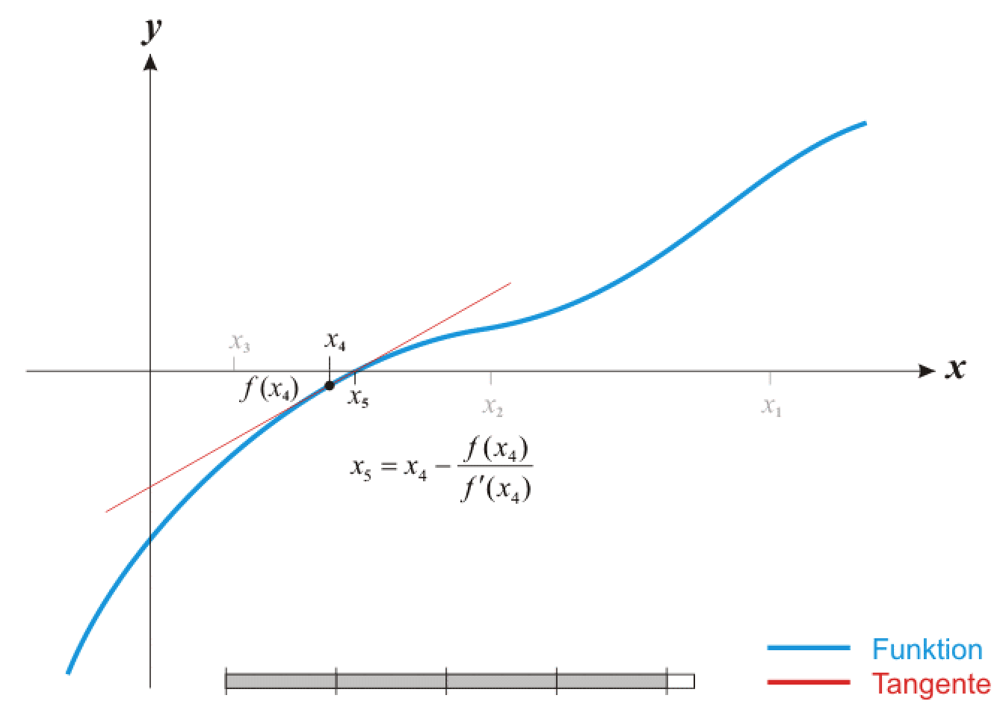
- ④、x4⇒x5
![]()
- ⑤、不断迭代,直到收敛,此时xn即为方程f(x)=0的根
牛顿迭代法的应用
x的平方根
题目来源:Leetcode
题目链接:Leetcode-69
题目描述:
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
示例 1:
输入: 4
输出: 2
示例 2:
输入: 8
输出: 2
说明: 8 的平方根是 2.82842…,
由于返回类型是整数,小数部分将被舍去。
解题思路
为了避免与f(x)中的x混淆,我们将题目中x的平方根记为m的平方根
- 明确目标:m的平方根是我们所要求的东西,因此若将这个问题套用到牛顿迭代法上,就是要找到一个函数f(x),使得这个函数的根为m
- 寻找目标函数:考虑函数f(x)=x2−m,其满足f(m)=m2−m=0,可以作为我们的目标函数。
- 推导迭代公式:将函数 f(x)=x2−m 和其导数 f′(x)=2x 代入牛顿迭代公式xn+1=xn−f′(xn)f(xn)中即可得到:
xn+1=21(xn+xnm).
- 开始迭代:选定初始值x0,可以为任意数字,不同的初始值只会影响收敛的快慢,最终都会收敛于方程f(x)=0的根。此处默认设x0=m,不断迭代,直到收敛。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution(object):
def mySqrt(self, m):
"""
:type m: int
:rtype: int
"""
if(m <= 1):
return m
sqrt = m
while(sqrt > m / sqrt):
sqrt = (sqrt + m / sqrt) // 2
return sqrt
|
![]()
![]()
![]()
![]()